Зачем надо делать закон нормального распределения

Переменная величина случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями. Наиболее полной, исчерпывающей характеристикой случайной величины является закон распределения.

Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина Х принимает определеное значение хi или попадает в некоторый интервал. Если случайная величина имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения.

Каждый закон распределения – это некоторая функция, полностью описывающая случайную величину с вероятностной точки зрения.

Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений, в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий. Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть, является, с математической точки зрения, не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

Выборочный коэффициент асимметрии используется для проверки распределения на симметричность, а также для грубой предварительной проверки на нормальность. Он позволяет отвергнуть, но не позволяет принять гипотезу нормальности. Коэффициент эксцесса (коэффициент островершинности) — мера остроты пика распределения случайной величины.

«Минус три» в конце формулы введено для того, чтобы коэффициент эксцесса нормального распределения был равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если вершина гладкая. случайной величины — числовая характеристика распределения данной случайной величины.

«Правда, чистая правда и статистика» или «15 распределений вероятности на все случаи жизни»

30 сентября 2016 в 10:46

1. ,
2. ,
3. ,

1. Tutorial

Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных.

Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика.

С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест к любым данным без проверки их нормальности.

Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста в ненавистников статистики. Попробуем поставить токи над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь. В первую очередь, данный материал будет интересен студентам, изучающим теорию вероятностей и статистику, хотя и «зрелые» специалисты смогут его использовать в качестве справочника.

В одной из следующих работ я покажу пример использования статистики для построения теста оценки значимости показателей биржевых торговых стратегий. В работе будут рассмотрены :

• ,
• ;
• ;
• ;
• ;
• ;

а также :

• ;
• .
• ;
• ;
• ;
• ;
• ;
• ;
• ;

В конце статьи будет задан для размышлений.

Свои размышления по этому поводу я изложу в следующей статье. Некоторые из приведённых непрерывных распределений являются частными случаями . Дискретные распределения используются для описания событий с недифференцируемыми характеристиками, определёнными в изолированных точках.

Проще говоря, для событий, исход которых может быть отнесён к некоторой дискретной категории: успех или неудача, целое число (например, игра в рулетку, в кости), орёл или решка и т.д. Описывается дискретное распределение вероятностью наступления каждого из возможных исходов события. Как и для любого распределения ( в том числе непрерывного) для дискретных событий определены понятия матожидания и дисперсии.

Однако, следует понимать, что матожидание для дискретного случайного события — величина в общем случае нереализуемая как исход одиночного случайного события, а скорее как величина, к которой будет стремиться среднее арифметическое исходов событий при увеличении их количества.

В моделировании дискретных случайных событий важную роль играет комбинаторика, так как вероятность исхода события можно определить как отношение количества комбинаций, дающих требуемый исход к общему количеству комбинаций. Например: в корзине лежат 3 белых мяча и 7 чёрных.

Нормальное распределение

Перейти к: , Плотность вероятностиЗеленая линия соответствует стандартному нормальному распределению Функция распределенияЦвета на этом графике соответствуют графику наверху Параметры

— ()

и

независимы и имеют нормальное распределение с математическими ожиданиями

и

и дисперсиями

и

соответственно, то

также имеет нормальное распределение с математическим ожиданием

и дисперсией

.

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:

1. — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.

Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в — это обобщение одномерного нормального распределения.

имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

1. Произвольная компонентов вектора
   

   имеет нормальное распределение или является константой.

Нормальный закон распределения

Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основопологающую роль в математической статистике.

Причинами это являются:

• Корректное использование предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и F-критерия Фишера требует нормального распределения экспериментальных данных.
• Многие можно успешно описать с помощью нормального закона распределения. Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
• Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
• Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.

Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.Абрахам де Муавр (1667– 1754) – английский математик, предложил формулу нормального распределения, описывающую биномиальное распределение с вероятностью 0,5. Эта формула появилась в работе А.Муавра «Доктрина случайностей».Карл Фридрих Гаусс (1777 – 1855) – немецкий математик, проводил исследования в области нормального распределения ошибок. Ввел это распределение как возникающее в результате многократных измерений движений небесных тел.Пьер-Симон де Лаплас (1749-1827) — французский математик, механик, физик и астроном.

П.-С. Лаплас обобщил результаты А. Муавра для произвольного биномиального распределения.Адольф Кетле (1796-1874) – бельгийский математик, одним из первых применил нормальный закон распределения случайной величины к анализу биологических и социальных процессов.Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение.

• нормального распределения совпадают и равны µ.
• Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
• Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
• нормального распределения равны нулю.

В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения.Нормированное отклонение рассчитывает по формуле:Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения.

Почему с нормальным распределением не все нормально

26 августа 2013 в 18:51

1. ,

Нормальное распределение (распределение Гаусса) всегда играло центральную роль в теории вероятностей, так как возникает очень часто как результат воздействия множества факторов, вклад любого одного из которых ничтожен.

Центральная предельная теорема (ЦПТ), находит применение фактически во всех прикладных науках, делая аппарат статистики универсальным. Однако, весьма часты случаи, когда ее применение невозможно, а исследователи пытаются всячески организовать подгонку результатов под гауссиану.

Вот про альтернативный подход в случае влияния на распределение множества факторов я сейчас и расскажу.

Краткая история ЦПТ. Еще при живом Ньютоне Абрахам де Муавр доказал теорему о сходимости центрированного и нормированного числа наблюдений события в серии независимых испытаний к нормальному распределению.

Весь 19 и начало 20 веков эта теорема послужила ученым образцом для обобщений. Лаплас доказал случай равномерного распределения, Пуассон – локальную теорему для случая с разными вероятностями.

И только в 1934 году Феллер поставил точку, показав, что существование моментов второго порядка, является и необходимым и достаточным условием.

ЦПТ можно сформулировать так: если случайные величины независимы, одинаково распределены и имеют конечную дисперсию отличную от нуля, то суммы (центрированные и нормированные) этих величин сходятся к нормальному закону.

Именно в таком виде эту теорему и преподают в вузах и ее так часто используют наблюдатели и исследователи, которые не профессиональны в математике. Что в ней не так? В самом деле, теорема отлично применяется в областях, над которыми работали Гаусс, Пуанкаре, Чебышев и прочие гении 19 века, а именно: теория ошибок наблюдений, статистическая физика, МНК, демографические исследования и может что-то еще. Но ученые, которым не достает оригинальности для открытий, занимаются обобщениями и хотят применить эту теорему ко всему, или просто притащить за уши нормальное распределение, где его просто быть не может.

Хотите примеры, они есть у меня.

Коэффициент интеллекта IQ. Изначально подразумевает, что интеллект людей распределен нормально. Проводят тест, который заранее составлен таким образом, при котором не учитываются незаурядные способности, а учитываются по-отдельности с одинаковыми долевыми факторами: логическое мышление, мысленное проектирование, вычислительные способности, абстрактное мышление и что-то еще.

Способность решать задачи, недоступные большинству,

Закон нормального распределения

Стр 18 из 102 Если испытывать много одинаковых деталей на какое-то одно свойство, то результат окажется следующим: – от 1% до 3% деталей покажут отличные, очень хорошие результаты; – от 3% до 7% – хорошие результаты; – от 80% до 90% – нормальные результаты; – от 3% до 7% – плохие результаты; -от 1% до 3% – безобразные, очень плохие результаты.

Так, если взять 100 хоккейных клюшек и провести испытания на их излом (класть клюшки по очереди на спинки двух стульев и бро­сать с высоты 1 метра гирю весом 10 кг ), то результаты окажутся приблизительно такими: – одна-три клюшки «не дрогнут», на них не останется даже следа от гири; – на трех-семи клюшках останутся вмятины от гири, но они даже «не прогнутся»; – 80-90 клюшек прогнутся и выпрямятся, то есть с ними ни­чего не случится; -три-семь клюшек треснут; – одна-три клюшки сломаются совсем. По научному такое поведение при испытаниях множества одина­ковых предметов называется ЗАКОНОМ НОРМАЛЬНОГО РАС­ПРЕДЕЛЕНИЯ. Законом нормального распределения пользуются как при разра­ботке различных образцов техники, приборов, так и при их произ­водстве на заводах.

Так, в своём быту вы сталкивались с тем, что купленная вами новая электролампочка иногда сразу же перегорала при её включении. Некоторые лампочки у вас в квартире не перего­рали годами, в отличие от множества «обычных» лампочек, которые перегорали через определённое время.

Этот закон действует и во всех природных явлениях.

Напри­мер, в сосновом лесу основная масса деревьев – нормальные, строй­ные сосны. Но среди множества нормальных сосен вы наверняка видели сосны-красавицы! Однако вы находили и кривые, уродливые сосны.

Поэтому этим законом можно пользоваться для оценки при­родных явлений.

действует и среди людей, а потому применим для оценки процессов, происходящих в человечес­ком обществе. Если определённое множество людей «испытывать на излом», то результаты окажутся такими, как уже было приведено выше: – 1%-3% – несгибаемые; – 3%-7% – стойкие; – 80%-90% – нормальные («согнулись» и «выпрямились»); – 3%-7% – дают «трещину»; – 1%-3% – «ломаются».

Такие «испытания» с оценками можно проводить в отношении всех качеств людей: – умные – дураки; – добрые – злые; – щедрые – жадные; – смелые – трусливые; – терпеливые – торопыги и т.д. К качествам людей относится и их социальная активность.

Со­гласно закону нормального распределения получается, что социаль­но-активных людей в нашем обществе где-то 5-7%. Такое же ко­личество вообще отстранились от участия в социальной жизни.

Основная масса людей (80-90%%) – «ни туды, ни сюды». Они вроде бы равнодушны к политике и общественной жизни, однако от­слеживают те процессы, которые им интересны, хотя в целом отно­сятся отстранено и активности не проявляют.

Это как ангел лаода­кийской церкви из библии: «не холоден и не горяч, а тёплый». Так вот, 5%-7% социально активных людей в основном и являются членами всех ныне существующих партий и обществен­ных организаций.

А их сейчас – несколько десятков! Так что всех социально-активных во исполнение планов «сил Запада» давно рас­тащили по частям.

Журнал ЖЖ

Закон нормального распределения, или как его еще называют – кривая Гаусса, является одним из основных столпов в теории вероятности.

Его применение можно проследить практически во всех сферах современного человеческого знания, от физики до философии. Я же попробую в кратком обзоре на примерах, объяснить как можно применить этот принцип, при аналитике народных процессов в социологии.

Ось Xявляется цифровым представлением этой самой градации и уходит от нуля в обе стороны до относительной бесконечности (но в некоторых случая она жестка ограничена). Ось Y является показателем величины вероятности значения из градации и может быть от нуля до одного.

Сложно? Нет, все просто, взгляните вот на этот график и вам станет все довольно ясно.Допустим, вы идете по улице, хотите спросить что-то умное у прохожего, и обращаясь к случайному человеку, вы можете быть уверены в том, что с максимально вероятностью он будет человеком среднего ума, в меньшей вероятности, что он будет дураком или умником и в практически минимальной возможности – гением или откровенным тупицей. Одним словом этот график показывает вероятностное распределение интеллектуальности общества.

Таким образом, обратившись к любой позиции на графике, можно сказать, какова вероятность при переборе людей, встретить гения, умного или дурака.

Естественно этот график является просто примером, и может не иметь никакого отношения к реальности. Для реальной же картины подобного рода, должен работать целый статистический комитет. Как можно понять из приведенного примера, график может деформироваться, в ту или иную сторону, и представлять уже иную вероятность.

Показанный же график, называется – Стандартным нормальным распределением, потому что такая форма кривой вероятности установлена самой природой. И если мы обратимся в мир биосферы, и будем оценивать разные вероятности, то обнаружим, что данная форма кривой будут доминировать. В определении ЗНР я указал, что ось Xуходит по обе стороны в бесконечность.

Дело в том, что оценка, каких либо общественных величин методом живой статистики, является явлением, находящемся только в настоящем времени. Общество не стоит на месте, оно постоянно движется, развивается или деградирует, поэтому сейчас оно одно, завтра другое, а значит, будет и другая форма и положение кривой Гаусса. Если не уходить с позиции стандартного нормального распределения, то для демонстрации

Нормальное распределение и его значение

Большинство случайных величин подчиняется определенному закону распределения, зная который можно предвидеть вероятности попадания исследуемой случайной величины в определенный интервал.

Такое предсказание весьма желательно при анализе экономических показателей, ведь в этом случае появляется возможность осуществить продуманную политику с учетом возможности возникновения той или иной ситуации. Законов распределения достаточно много, поэтому мы ограничимся рассмотрением лишь тех законов, которые наиболее активно встречаются в экономической теории, особенно в эконометрике.

Одним из наиболее часто встречающихся распределений является нормальное распределение (его еще называют распределением Лапласа-Гаусса, или просто распределением Гаусса.). Оно играет огромную роль в теории вероятностей и ее приложениях. Плотность нормального распределения имеет вид

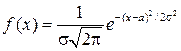
, (2.18) а функция нормального распределения имеет вид

.

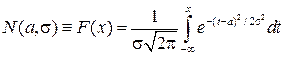
(2.19) Если a=0, s=1, то получим

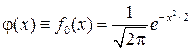
, (2.20)

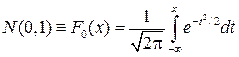
(2.21) стандартное нормальное распределение. Эту функцию можно записать в виде

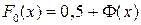
, где

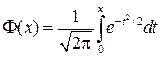
(2.22) есть функция Лапласа. Между произвольной функцией нормального распределения и стандартным распределением (соответственно и функцией Лапласа) существует взаимосвязь:

.

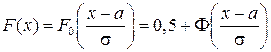
(2.23) Для плотности нормального распределения имеем

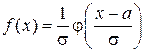
. (2.24) Для плотности стандартного нормального распределения j(x) и функции Лапласа F(x) существуют обширные таблицы.

Однако здесь нужно иметь в виду, что иногда вместо рассмотренных функций используют функци.

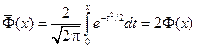
. Отметим, что для нормального распределения M[X] = a, D[X] = s2, т.е.

нормальное распределение характеризуется двумя параметрами: a, имеющим смысл математического ожидания, и s, имеющим смысл среднего квадратичного отклонения. Вероятность того, что нормально распределенная случайная величина X примет значение, принадлежащее интервалу (a, b), имеет вид

.

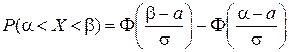
(2.25) Вероятность того, что отклонение случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа d, равна

.

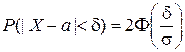
Нормальный закон распределения, или Распределение Гаусса

Среди всех законов в теории вероятностей нормальный закон распределения встречается чаще всего, в том числе чаще, чем равномерный.

Возможно, такое явление имеет глубокую фундаментальную природу. Ведь этот вид распределения наблюдается и тогда, когда в представлении диапазона случайных величин участвуют несколько факторов, каждый из которых влияет по-своему. Нормальное (или гауссово) распределение в таком случае получается вследствие сложения разных распределений.

Именно благодаря широкому распространению нормальный закон распределения и получил свое название.Всякий раз, когда мы говорим о какой-либо будь то месячная норма осадков, доход на душу населения или успеваемость в классе, при вычислении ее значения, как правило, используется нормальный закон распределения.

Это называется и на графике соответствует максимуму (обычно обозначается как M).

При правильном распределении кривая симметрична относительно максимума, однако в реальности так бывает не всегда, и это допустимо.Чтобы описать нормальный закон распределения случайной величины, также необходимо знать среднеквадратичное отклонение (обозначается σ – сигма). Оно задает форму кривой на графике.

Чем больше σ, тем более пологой будет кривая. С другой стороны, чем меньше σ, тем точнее определяется среднее значение величины в выборке. Поэтому при больших среднеквадратичных отклонениях приходится говорить, что среднее значение лежит в определенном диапазоне чисел, а не соответствует какому-либо числу.Как и прочие законы статистики, нормальный закон распределения вероятностей проявляет себя тем лучше, чем больше выборка, т.е.

количество объектов, которые участвуют в измерениях. Однако здесь проявляется еще один эффект: при большой выборке становится очень малой вероятность встретить определенное значение величины, в том числе среднее.

Значения лишь группируются возле среднего. Поэтому правильнее говорить, что случайная величина будет близка определенному значению с такой-то долей вероятности.Определить, насколько велика вероятность, и помогает среднеквадратичное отклонение.

В интервал «три сигмы», т.е. M +/- 3*σ, укладывается 97,3 % всех величин в выборке, а в интервал «пять сигм» — около 99 %.

обычно используются для того, чтобы определить, когда это нужно, максимальное и минимально значение величин в выборке. Вероятность того, что значение величины выйдет из интервала пяти сигм, ничтожно мала. На практике обычно пользуются интервалом трех сигм.Нормальный закон распределения может быть многомерным.

При этом принимается, что некий объект обладает несколькими независимыми параметрами, выраженными в одной единице измерения.

Например, отклонение пули от центра мишени по вертикали и по горизонтали при стрельбе будет описываться двумерным нормальным распределением. График такого распределения в идеальном случае похож на фигуру вращения плоской кривой (гауссианы), о которой говорилось выше.

1 мая, 2013 Статья закончилась. Вопросы остались? Комментарии 0 Следят за новыми комментариями

Большая Энциклопедия Нефти и Газа

Cтраница 1 Нормальный закон распределения полностью определяется двумя числовыми характеристиками — математическим ожиданием и дисперсией или средним квадрати-ческим отклонением.

Нормальный закон распределения наблюдается в тех случаях, когда на признак явления действует много факторов, каждый из которых мало связан с большинством других, и влияние каждого фактора на конечный результат существенно меньше суммарного влияния всех остальных факторов. Нормальный закон распределения описывает поведение объектов, которым типичен износ, причем все отказы однородны по качеству и имеют малый разброс износа. Нормальный закон распределения наработки характерен для постепенного нарастания отказов, вызванных износом и старением.

Он также применим при большом числе случайных факторов, когда влияние каждого из них незначительно по сравнению с совокупностью влияний остальных факторов. Нормальный закон распределения находит очень широкое применение в науке и технике. Нормальный закон распределения занимает особое место среди других законов распределения.

Нормальный закон распределения ( часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает особое место среди других законов распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Нормальный закон распределения находит также применение при анализе многих типов ошибок экспериментальных измерений и при оценке характеристик оборудования и систем.

Нормальный закон распределения дает достаточно точные результаты при большом числе испытаний.

При л 20 и при значениях Р, отличающихся от 0 и 1, полученные результаты нормального закона и биномиального распределения практически не отличаются.

Нормальный закон распределения свободен от указанных недостатков биномиального распределения.

И главное достоинство, что нормальный закон распространяется на очень большой класс случайных явлений и используется во многих практических случаях. Нормальный закон распределения, законы равной вероятности и треугольника применяются при практических расчетах размерных цепей наиболее часто.

Нормальный закон распределения играет весьма важную роль в теории математической обработки результатов измерений и потому занимает среди других законов распределения особое место. Большинство встречающихся на практике случайных величин ( например, погрешности измерений) можегбыть представлено как сумма весьма большого числа сравнительно малых слагаемых, каждое из которых обусловлено действием отдельной причины, не зависящей от остальных. Теоретически и практически установлено, что такие суммы подчиняются ( в асимптотике) закону нормального распределения.

Нормальный закон распределения наиболее часто встречается на практике.

В силу важности этого закона мы изучим подробно его несколько позже.

Нормальный закон распределения (стр.

1 из 3)

СОДЕРЖАНИЕ 1. ВВЕДЕНИЕ 6 1. ОСНОВНЫЕ ПАРАМЕТРЫ И ОПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ 8 1.1.

Нормальное распределение 8 1.2.

Статистическая гипотеза 8 1.3. Ошибки первого и второго рода. Уровень значимости 9 1.4. Степень свободы параметра 10 1.5.

Критическая область. Область принятия гипотезы. 10 1.6. Критерий Стьюдента 11 1.7.

Критерий Фишера 13 1.8. Критерий Кохрэна 15 1.9. Критерий Пирсона 15 2. ХАРАКТЕРИСТИКА ПАКЕТА EXCELL 19 3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 21 4.

4. ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ДАННЫХ В ВЫБОРКЕ 24 4. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ДАННЫХ В ВЫБОРКЕ 26 ЗАКЛЮЧЕНИЕ 28 ЛИТЕРАТУРА 29 Нормальное (гауссовское) распределение занимает центральное место в теории и практике вероятностно-статистических исследований.

В качестве непрерывной аппроксимации к биномиальному распределению его впервые рассматривал А.Муавр в 1733 г.

Через некоторое время нор­мальное распределение снова открыли и изучили К.Гаусс (1809 г.) и -П.Лаплас, которые пришли к нормальной функции в связи с ра­ботой по теории ошибок наблюдений. Цельих объяснения механизма формирования нормально распределенных случайных величин заключается в следующем.

Постулируется, что зна­чения исследуемой непрерывной случайной величины формируются под воздействием очень большого числа независимых случайных факторов, при­чем сила воздействия каждого отдельного фактора мала и не может прева­лировать среди остальных, а характер воздействия — аддитивный (т.е. при воздействии случайного фактора F на величину а получается вели­чина ___________, где случайная «добавка» ______ мала и равновероятна по знаку). Во многих случайных величинах, изучаемых в технике и других областях, естественно видеть суммарный аддитивный эффект большого числа независимых причин.

Но центральное место нормального закона не следует объяснять его универсальной приложимостью.

В этом смысле нормальный закон — один из многих типов распределения, имеющихся в природе, однако с относительно большим удельным весом практической приложимости. Однако полнота теоретических исследований, относящихся к нормаль­ному закону, а также сравнительно простые математические свойства де­лают его наиболее привлекательным и удобным в применении.

Даже в слу­чае отклонения исследуемых экспериментальных данных от нормального закона существует, по крайней мере, два пути его целесообразной эксплуатации: во-первых, использовать нормальный закон в качестве пер­вого приближения (при атом нередко оказывается, что подобное допуще­ние дает достаточно точные с точки зрения конкретных целей исследова­ния результаты); во-вторых. подобрать такое преобразование исследуемой случайной величины, которое видоизменяет исходный «не нормальные» закон распределения, превращая его в нормальный.

Удобно для статистических приложений и свойство «самовоспроизводимости» нормального закона, заключающееся в том, что сумма любого числа нормально распределенных случайных величин тоже подчиняется нормальному закону распределения.

Нормальное распределение, или закон гаусса

Стр 83 из 118Закон больших чисел, как мы выяснили, играет огромную роль в социоло­гии и статистике.

Без него не могли бы возникнуть и успешно развиваться на­уки, занятые изучением массового поведения. Закон больших чисел гласит, что в результате взаимопогашения случайных отклонений средние, исчисленные для величин одного и того же вида, становятся типичными, отражающими действие постоянных и существенных факторов в данных условиях времени и места.

Он утверждает господство средне-типичного, а это как раз то, что интересует со­циологию. Но он не говорит ничего о том, как велика та часть населения, кото­рая составляет в нормально развивающемся обществе большинство. На этот вопрос отвечает другой закон — нормального распределения, или закон Гаусса.

Гаусс Карл Фридрих (1777—1855) —немецкий математик, иностранный член-корреспондент (1802) и иностранный почетный член (1824) Пе­тербургской АН. Еще при жизни Гаусс был удостоен почетного титула «принц математиков». Он блестяще находил практические применения результатам своих фундаментальных исследований и из конкретных за­дач прикладных областей умел извлекать проблемы, представляющие интерес для фундаментальной науки.

В области прикладной математики он не только получил ряд важных результатов, но и создал новые на- Посмотрев на все это подобным образом, я понял, как глупо я себя вел.

В тот же момент я решил прекратить беспокоиться и всегда при­менять закон больших чисел. С тех пор я забыл про свою язву желудка». Когда Эл Смит был губернатором штата Нью-Йорк, я слышал, как он отражал нападки своих по­литических противников, повторяя снова и снова: «Давайте изучим факты.

давайте изучим факты». Затем он начинал приводить факты. В следующий раз, если вы или я будем беспокоиться о том, что может случиться, послушаемся мудрого старого Эла Смита: давайте изучим факты и решим, есть ли повод для нашего мучительного беспокойства. Именно так поступал Фредерик Дж.

Малстедт, когда испугался, что уже лежит в могиле. Вот что он рассказал мне в период занятий на моих кур­сах для обучения взрослых в Нью-Йорке: «В начале июня 1944 года я находился в одиноч­ном окопе вблизи Омаха-Бич.

Я служил в 999 роте связи, и мы только что «окопались» в Нормандии. Когда я посмотрел на этот одиночный окоп (он выглядел как яма прямоугольной формы в земле), я сказал себе: «Похоже на могилу». Когда я лег в его и попытался заснуть, мне показалось, что я Действительно в могиле.

Я невольно подумал: Наверное, это и в самом деле моя могила». 11 часов утра начались налеты немецких бом-РДировщиков, и на нас посыпались бомбы.

Я одеревенел от страха. В первые две или три ночи я совсем не мог спать. К четвертой или пятой ночи я был почти в состоянии нервного шока.

Я понял, что необходимо что-то сделать, иначе я сойду с ума.

Тогда я напомнил себе, что прошло пять ночей, а я все еще жив, и все были живы в нашем подразделении. Только двое были ранены, да и то не немецкими бомбами, а осколками снарядов наших собственных зенит­ных орудий.