Правилм решентч кравнентя с еорнем
Оглавление:
Иррациональные уравнения на примерах
Иррациональными называют уравнения в которых неизвестная величина находится под знаком корня определенного степени. Простейшие иррациональные уравнения решаются или подъемом в степень или заменой .
Сложные иррациональные уравнения сводятся к предыдущим некоторыми искусственными методами . Например, такое на первый взгляд сложное уравнениесводится к квадратному заменой
Зачастую при раскрытии иррациональности используют формулу сложного радикала
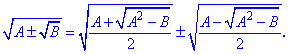
Стоит отметить, что при решении иррациональных уравнений необходимо определять область допустимых значений.
Кроме того следует производить проверку, подставляя найденные значения неизвестных в исходное уравнение, поскольку при возведении в степень мы увеличиваем степень уравнения что может привести к появлению посторонних корней.Перейдем к вычислениям.Пример 1. Найти решение уравнения
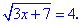
Решение:Находим область допустимых значений
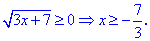
Подносим обе части уравнения в квадрат и решаем
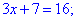
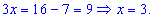
Получили решение x=3.————————-Пример 2. Найти решение уравнения
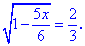
Решение:ОДЗ для уравнения
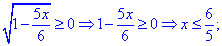
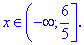
Раскрываем иррациональность уравнения и находим
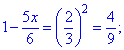
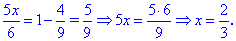
Он принадлежит области допустимых значений , то есть — является решением.————————-Пример 3.
Решить уравнение
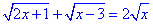
Решение:Находим область допустимых значений
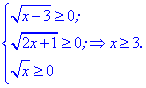
ОДЗ:
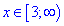
По описанной схеме подносим обе части в квадрат чтобы избавиться иррациональностиПереносим все слагаемые кроме корней в правую часть и упрощаем
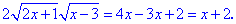
Для раскрытия иррациональности снова выполняем возведения в квадрат и упрощение
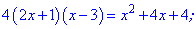
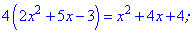
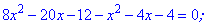
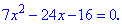
Получили квадратное уравнение, корни которого находим с помощью дискриминанта
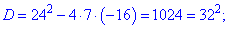
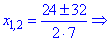
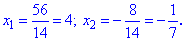
Второй корень не принадлежит области допустимых значений . Эту проверку следует выполнять всегда , иначе получите
Как находить корень уравнения
Если есть две величины, а между ними стоит знак равенства, то это пример, который называют уравнением.
Высчитав неизвестное, мы узнаем корень. Чтобы рассекретить это неизвестное, придется потрудиться над вычислением. 1 Понятнее будет, если возьмем в работу конкретное уравнение: x+10=16-2х.
Оно относится к линейным, составляют его свободные члены и неизвестное х.
Разносим эти составляющие в разные стороны от знака равенства.
Теперь уравнение приобрело такой вид: 2х + х = 16 – 10 или 3х = 6; х = 2. Результат: Х = 2. 2 Немного больший запас знаний нужно для вычисления корня в примере, где искомое в квадрате.
Это уравнение квадратное и отличие его от линейного в том, что результатов может быть 1 или 2 или обнаружится, что корней 0.
Чтобы понять лучше, решим уравнение: Х, возведенный в квадрат, умножить на 3 + 3Х = 90.
Делаем так, чтобы справа образовался 0: Х2 х 3 + 3Х -90 = 0.
Числа перед Х – коэффициенты 1, 3, 3. Требуется определение дискриминанта: возводим в квадрат 3 – второй коэффициент и отнимаем произведение 1 и 3.
Для подсчета 1 корня ко второму коэффициенту со знаком – прибавляем корень из D и делим это на удвоенный первый коэффициент: -3 + квадратный корень из 16, делим на 2. Выйдет 1/2. Вычисление второго аналогично, только корень из D вычитаем. Имеем в результате – 3 целых и 1/2.
3 Сложнее квадратного уравнение кубическое. Вид у него такой: х3-3х2-4х+20=0. Подбираем число, на которое можно поделить свободный член, чтобы слева появился 0.
Делители для 20 – это ±1, ±2, ±4, ±5, ± 10, ± 20. Получается, что это делитель 5, он же и один из искомых корней.
Остается решить квадратное уравнение и все корни известны. Вот и все премудрости. Нет ничего сложного, но чтобы было совсем просто, можно воспользоваться онлайн-калькулятором.
Иррациональные уравнения.
Исчерпывающий гид (2020)
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш.
Как это сделать в твоем браузере написано здесь: Содержание раздела Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень. А вот как это выглядит: ; . Сначала разберемся что такое , а потом поймем что же из себя представляет решение иррациональных уравнений. Итак, что такое рациональные уравнения, а что – иррациональные:
- – вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
- тут вот степень, но она с целым показателем степени ( – целое число) – значит это тоже рациональное уравнение;
- как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
- а это – рациональное;
- – тоже рациональное, т.к. ;
- – а с ним поосторожнее, степень-то дробная, а по свойству корней , как ты помнишь корня в рациональных уравнениях не бывает. Надеюсь, теперь ты сможешь различать, к какому виду относится уравнение.
- даже уравнение с отрицательным показателем степени тоже является рациональным, ведь по сути – это ;
Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо!
Вся сложность в корнях, так? Так избавься от них, вот и все дела! Если еще не догадался как, то я подскажу – просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение, но проверяй все корни, позже поймешь почему.
Как рациональные уравнения решать помнишь? Если забыл, то советую почитать ().
Если читать лень, напомню вкратце.
Для верного решения рациональных уравнений, ты должен придерживаться следующего руководства:
- Решить получившееся целое уравнение;
- Найти общий знаменатель дробей и умножить на него обе части уравнения;
- Определить ОДЗ;
- Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);
- Исключить из его корней те, которые обращают в ноль знаменатель дробей.
Вроде все объяснил, давай решать, математика слов не любит. Вот такое вот уравнение , корень из икса видишь? Значит, какое уравнение? Верно, оно иррациональное!
Что дальше? Избавляемся от корней, поскольку корень второй степени, то обе части уравнения возводим в квадрат и упрощаем: Вот и все, почти все, что осталось сделать?
Правильно, решая иррациональное уравнение, обязательно надо проводить проверку полученных корней! Подставим в исходное уравнение, именно в исходное уравнение, потому, что нам нужно найти его корни, а возведя в квадрат, мы могли получить посторонние корни (об этом позже). тут все верно. Давай еще одно .
О том, что это иррациональное уравнение, думаю, ты и сам знаешь. Как и раньше возводим в квадрат обе части: , упрощаем, . Проверка, подставим в исходное уравнение: – вот это да, ничего тебя тут не смущает?
Под квадратным
Решение неравенств
,
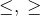
.
Знаки > называются знаками строгого неравенства, а знаки — знаками нестрогого неравенства. Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством. ОПРЕДЕЛЕНИЕ Решением неравенства называется значения переменной, при котором неравенство становится верным.
Решить неравенство — это значит найти множество всех его решений Неравенства называют равносильными, если они имеют одно и тоже множество решений.
- Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
- Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
- Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.
В зависимости от того, какие функции входят в неравенство, различают , , дробно-рациональные, , , , .
Если требуется все общие решения двух или нескольких неравенств, то .
Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. ПРИМЕР 1 Задание Решить неравенство
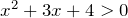
Решение Рассмотрим квадратное уравнение
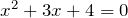
и найдем его дискриминант
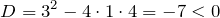
Поскольку дискриминант отрицательный, то парабола
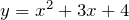
(рис.
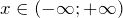
.
Ответ ПРИМЕР 2 Задание Решить неравенство
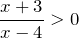
Решение Дробь будет положительной в том случае, когда числитель и знаменатель одного знака, т.е.
возможны два случая
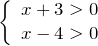
или . Таким образом, необходимо найти решение совокупности
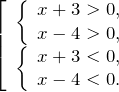
Решим каждую систему неравенств отдельно: 1.
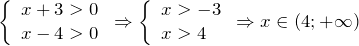
.
Квадратный корень. Исчерпывающий гид (2020)
Важное замечание!
Какие числа можно возвести в квадрат и получить при этом ? Вспомнив таблицу умножения, ты легко дашь ответ: и (ведь при перемножении двух отрицательных чисел получается число положительное)!
Для упрощения математики ввели специальное понятие квадратного корня и присвоили ему специальный символ Давай разберемся с корнем до конца.
СОДЕРЖАНИЕ Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа называется такое неотрицательное число, квадрат которого равен .
. А почему же число должно быть обязательно неотрицательным? Например, чему равен ? Так-так, попробуем подобрать. Может, три? Проверим: , а не .
Может, ? Опять же, проверяем: . Ну что же, не подбирается? Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число!
Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным! Однако ты наверняка уже заметил, что в определении сказано, что
«квадратным корнем из числа называется такое неотрицательное число, квадрат которого равен »
. А в самом начале мы разбирали пример , подбирали числа, которые можно возвести в квадрат и получить при этом , ответом были и , а тут говорится про какое-то «неотрицательное число»!
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат. Итак, вкратце на примере, нужно ли ставить «плюс-минус» (этот наглядный пример привёл наш читатель Игорь, спасибо ему за это): Пусть есть две ситуации: 1) 2) В первом случае у нас квадратное уравнение и его решением будет (уже видно отличие от второго случая) и далее получаем два корня Во втором случае у нас НЕТ квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8.
А теперь попробуй решить такое уравнение . Уже все не так просто и гладко, правда?
Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: – не подходит.
Двигаемся дальше ; – меньше трех, тоже отметаем.
Решение иррациональных неравенств
В этой статье я расскажу об одном эффективном способе решения иррациональных неравенств.
То есть таких неравенств, которые содержат неизвестную величину под знаком корня.
Данный материал очень редко изучается в школа.
Разве что в школе с углублённым изучением математики, да и то не всегда. А ведь научиться решать иррациональные неравенства, используя этот способ, очень важно.
Поэтому дочитайте эту статью до конца или посмотрите мой видеоурок (ссылка ниже в тексте). Информация, которую вы получите, может очень пригодиться при сдаче ОГЭ, ЕГЭ или вступительных экзаменов по математике. Иррациональные неравенства, как и любые другие, изучаемые в школьном курсе математики, можно решить с помощью .
Но есть более простой и эффективный способ. Разберёмся, в чём он заключается. Все наиболее часто встречающиеся иррациональные неравенства из школьного курса математики можно условно разделить на два типа: 1.
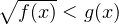
или
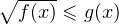
.
2.
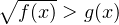
или
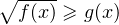
. Здесь
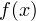
и
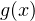
— некоторые выражения относительно переменной
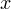
.
Разберём отдельно решение каждого из этих двух типов иррациональных неравенств.
Рассмотрим внимательно неравенство .
Как уже отмечалось, и — это некоторые выражения относительно переменной . Но при определённых значениях эти выражения будут принимать какие-то определённые значения. Наша задача состоит в том, чтобы найти такие значения переменной , при которых значение выражения будет больше значения выражения
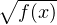
.
Извините, что я говорю очевидные вещи. В данной статье я решил объяснить всё предельно подробно. Если эти разъяснения кажутся вам излишними, вы можете пропустить их и перейти непосредственно к примерам в красных рамочках.
Чтобы избавиться от корня, нужно возвести обе части неравенства в квадрат.
Тогда неравенство примет вид:
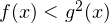
.
Но просто так, без соблюдения определённых правил, этого делать нельзя. Почему? Представьте, что при каком-то значении значение выражения равно, скажем,
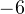
, а значение выражения равно,
Предел функции с корнями
Среди примеров пределов функции часто встречаются функции с корнями, которые не всегда понятно как раскрывать.
Проще когда есть пример границе с корневой функцией вида
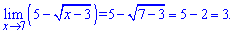
Решение подобных пределов просто и понятно каждому. Трудности возникают если есть следующие примеры функций с корнями.Пример 1. Вычислить предел функции
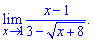
При прямой подстановке точки x = 1 видно что и числитель и знаменатель функции
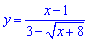
превращаются в ноль, то есть имеем неопределенность вида 0/0.
Для раскрытия неопределенности следует умножить выражение, содержащее корень на сопряженное к нему и применить правило разности квадратов. Для заданного примера преобразования будут следующими
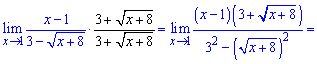
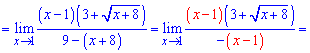
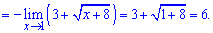
равен 6. Без приведенного правила ее трудно было бы найти.
Рассмотрим подобные примеры вычисления границы с данным правиломПример 2.
Найти предел функции
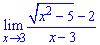
Убеждаемся что при подстановке x = 3 получаем неопределенность вида 0/0. Ее раскрываем умножением числителя и знаменателя на сопряженное к числителю.
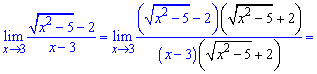
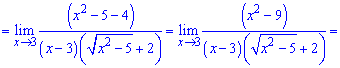
Далее числитель раскладываем согласно правилу разности квадратов
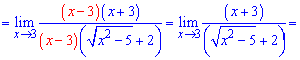
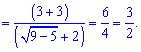
Вот так просто нашли предел функции с корнями.Пример 3.
Определить предел функции
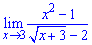
Видим, что имеем неопределенность вида 0/0. Избавляемся ирациональносьти в знаменателе
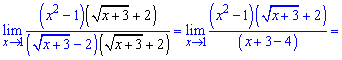
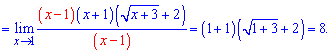
Предел функции равна 8.
Теперь рассмотрим другой тип примеров, когда переменная в переделе стремится к бесконечности.Пример 4. Вычислить предел функции
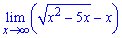
Много из Вас не знают как найти предел функции.
Ниже будет раскрыта методика вычислений.
Имемем предел типа бесконечность минус бесконечность.
Умножаем и делим на сопряженный множитель и используем правило разности квадратов
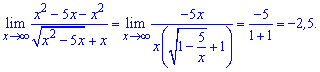
Границ функции равна -2,5.Вычисление подобных пределов фактически сводится к раскрытию иррациональности , а затем подстановке переменнойПример 5. Найти предел функции
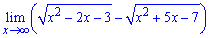
Предел эквивалентен — бесконечность минус бесконечность
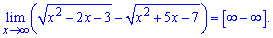
. Умножим и разделим на сопряженное выражение
Как решать примеры с корнями
1 декабря 2011 Автор КакПросто!
Корнем n степени из числа называют такое число, которое при возведении в эту степень даст то число, из которого извлекается корень.
Чаще всего, действия производятся с корнями квадратными, которые соответствуют 2 степени. При извлечении корня часто невозможно найти его явно, а результатом является число, которое невозможно представить в виде натуральной дроби (трансцендентное).
Но используя некоторые приемы, можно значительно упростить решение примеров с корнями. Статьи по теме:
Иррациональные неравенства. Исчерпывающий гид (2020)
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: Иррациональным называется неравенство, содержащее переменную под знаком радикала (корня).
Чтобы хорошо понять, о чем здесь пойдет речь, повтори темы: СОДЕРЖАНИЕ Помнишь, что такое ОДЗ? ОДЗ (область допустимых значений) неравенства или неравенств – это множество значений переменной, при которых обе части данного неравенства (или неравенств) имеют смысл. Например, в уравнении присутствует квадратный корень.
А квадратный корень не имеет смысла, если подкоренное выражение отрицательно. То есть, в данном случае ОДЗ – это решения неравенства . Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.
Взять, например, такую задачу: .
При возведении в квадрат получаем , то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина? Но в некоторых случаях это может быть очень полезно. Более того, иногда можно решить пример просто найдя ОДЗ.
Например: . Но ведь мы помним, что квадратный корень всегда неотрицателен. Поэтому он всегда будет больше .
Значит, решением задачи будет ОДЗ: .
Ответ: . Естественно, знак неравенства может быть и нестрогим. Здесь и далее большими буквами , , , и т.д. я буду обозначать не переменные или параметры, а целые выражения, содержащие переменную.
Так, общая запись соответствует, например, уравнению : здесь и .
Как решить такое неравенство? Для начала вспомним, что функция – монотонна, то есть, чем больше подкоренное выражение, тем больше сам корень. Поэтому из двух корней больше тот, у которого подкоренное выражение больше.
Но недаром мы недавно вспоминали про ОДЗ. Есть ли какие-нибудь ограничения в этом неравенстве?
Действительно, чтобы неравенство имело смысл, необходимо, чтобы оба подкоренных выражения были неотрицательны: Но поскольку первое выражение больше второго, достаточно потребовать неотрицательности только второго: или Примеры (реши сам):
Ответы: 1.
Применим только что выученное правило: 2. . 3. . Все понятно в этих решениях? Если нет, значит ты скорее всего не повторил тему .
Корень всегда принимает неотрицательные значения, поэтому, он влияет на это неравенство, только если равен нулю.
То есть нужно ограничить корень, чтобы он не был равен нулю, а в остальном – дело за выражением . И не забываем про ОДЗ, подкоренное выражение неотрицательно.
А если оно неотрицательно, и при этом не должно быть равно нулю, то оно строго болше нуля: или Примеры (реши сам):
Ответы:
В случае нестрогого неравенства условие, что подкоренное выражение не равно нулю теперь лишнее.
Но это только добавило нам проблем, ведь при этом выражение может быть любым. Значит, надо отдельно рассмотреть случай, когда корень равен нулю: или Примеры (реши сам): 1.
Решение квадратных уравнений
6 июля 2011 Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет.
Умение решать их совершенно необходимо. Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0. Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Имеют два различных корня.
- Имеют ровно один корень;
- Не имеют корней;
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен.
Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac. Эту формулу надо знать наизусть.
Откуда она берется — сейчас неважно.
Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение.
А именно:
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
- Если D < 0, корней>
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают.
Взгляните на примеры — и сами все поймете: Задача. Сколько корней имеют квадратные уравнения:
- 5×2 + 3x + 7 = 0;
- x2 − 6x + 9 = 0.
- x2 − 8x + 12 = 0;
Выпишем коэффициенты для первого уравнения и найдем дискриминант:a = 1, b = −8, c = 12;D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16 Итак, дискриминант положительный, поэтому уравнение имеет два различных корня.
Аналогично разбираем второе уравнение:a = 5; b = 3; c = 7;D = 32 − 4 · 5 · 7 = 9 − 140 = −131. Дискриминант отрицательный, корней нет.
Осталось последнее уравнение:a = 1; b = −6; c = 9;D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один. Обратите внимание, что для каждого уравнения были выписаны коэффициенты.
Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество. Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты.
Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам: Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом.
Наконец, если D < 0, корней нет — ничего считать не> Задача. Решить квадратные уравнения:
- x2 − 2x − 3 = 0;
- x2 + 12x + 36 = 0.
- 15 − 2x − x2 = 0;
Первое уравнение:x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;D = (−2)2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их: Второе уравнение:15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;D = (−2)2 − 4 · (−1) · 15 = 64. D > 0 ⇒ уравнение снова имеет два корня.
Как решать уравнения с корнями
25 февраля 2011 Автор КакПросто! Иногда в уравнениях встречается знак корня.
Многим школьникам кажется, что решать такие уравнения «с корнями» или, правильнее выражаясь, иррациональные уравнения очень сложно, но это не так. Статьи по теме:
Степенью называется выражение вида . Здесь — основание степени, — показатель степени.
Проще всего определяется степень с натуральным (то есть целым положительным) показателем. По определению, . Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы. Возвести число в квадрат — значит умножить его само на себя.
. Возвести число в куб — значит умножить его само на себя три раза. . Возвести число в натуральную степень — значит умножить его само на себя раз: Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным. По определению,
.
Это верно для . Выражение 00 не определено. Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например, Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени.
Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня. Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел.
Выражение
для нас сейчас имеет смысл только при
. Выражение всегда неотрицательно, т.е.
.
Например, . Свойства арифметического квадратного корня: Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ; , так как ; , так как . Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например, Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел. Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.